Answer:
(a) water height =408.66 in.
(b) mercury height=30.04 in.
Step-by-step explanation:
Given: P=14.769 psi ( 1 psi= 6894.76
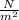 )
)
we know that
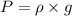
where
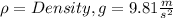
h=height.
Given that P=14.769 psi ⇒P= 101828.6 7
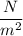
(a)
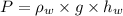
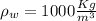
⇒101828.67=
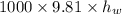
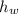 =10.38 m
=10.38 m
So water barometer will read 408.66 in. (1 m=39.37 in)
(b)
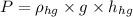
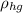 =13600
=13600
So 101828.67=
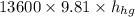
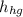 =0.763 m
=0.763 m
So mercury barometer will read 30.04 in.