Question

An inspector samples four PC’s from a steady stream of computers that is known to be 12% nonconforming. What is the probability of selecting two nonconforming units in the sample? Write your answer to 3 decimal places in the format: x.xxx

Answer 1

Answer: 0.067

Explanation:

Binomial distribution formula :-

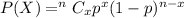`P(X)=^nC_xp^x(1-p)^(n-x)`, here P(x) is the probability of getting success in x trials , n is total number of trials and p is the probability of getting success in each trial.

Given : n = 4 , p = 12 % = 0.12 and x =2

Then ,
`P(2)=^4C_2(0.12)^2(1-0.12)^(4-2)`

`\Rightarrow\ P(2)=(4!)/(2!2!)(0.12)^2(0.88)^2=0.06690816\approx0.067`

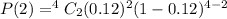
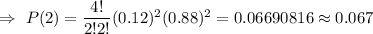
∴ The probability of selecting two nonconforming units in the sample = 0.067