Answer:
Throat diameter
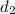 =28.60 mm
=28.60 mm
Step-by-step explanation:
Bore diameter
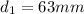 ⇒
⇒
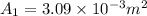
Manometric deflection x=235 mm
Flow rate Q=240 Lt/min⇒ Q=.004
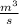
Coefficient of discharge
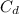 =0.8
=0.8
We know that discharge through venturi meter
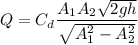
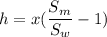
 =13.6 for Hg and
=13.6 for Hg and
 =1 for water.
=1 for water.
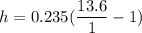
h=2.961 m
Now by putting the all value in
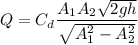
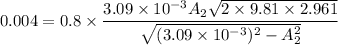
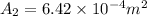
⇒
 =28.60 mm
=28.60 mm
So throat diameter
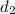 =28.60 mm
=28.60 mm