Question

A thick cylindrical pipe of outside diameter 300mm and internal diameter 200mm is subjected to an internal fluid pressure of 14 N/mm2. Determine the maximum hoop stress developed in the cross section. What is the percentage error if the maximum hoop stress is calculated by the equations for thin cylinder?

Answer 1

Answer:36.4 MPa

Step-by-step explanation:

External diameter(
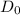`D_0`)=300mm

Internal diameter(
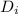`D_i`)=200mm

Internal Pressure(
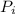`P_i`)=14N/
`mm^2`

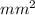
Now Hoop stress for Thick cylinders is given by

`\sigma _h`=
`(P_ir_i^2)/(r_0^2-r_i^2)\left ((r_0^2)/(r^2)+1\right )`

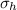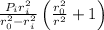
Maximum hoop stress will be develop at
`r=r_i`

`\sigma _h=36.4 MPa`

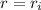
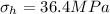
Now if we consider it as thin cylinder then Hoop stress is given by

`\sigma _h`=
`(P_(i)D)/(2t)`

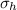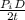
Where thickness =50 mm

`\sigma _h`=
`(14* 300)/(2* 50)`

`\sigma _h=42MPa`

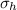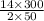
% error=
`(42-36.4)/(36.4)`
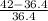
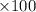`* 100`=15.38%