Question

Air at 293k and 1atm flow over a flat plate at 5m/s. The plate is 5m wide and 6m long. (a) Determine the boundary layer thickness 1m from the leafing edge. (b) Determine the critical distance Xc from the leading edge. if transition occur at a Reynold number of 100000(c) Repeat part (a) 3m from leading edge (d) Find the force exerted on the section of the plate where the flow is laminar (e) Determine the force exerted one one side of the entire plate

Answer 1

a). 8.67 x
`10^(-3)` m

b).0.3011 m

c).0.0719 m

d).0.2137 N

e).1.792 N

Step-by-step explanation:

Given :

Temperature of air, T = 293 K

Air Velocity, U = 5 m/s

Length of the plate is L = 6 m

Width of the plate is b = 5 m

Therefore Dynamic viscosity of air at temperature 293 K is, μ = 1.822 X
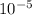`10^(-5)` Pa-s

We know density of air is ρ = 1.21 kg /
`m^(3)`

Now we can find the Reyonld no at x = 1 m from the leading edge

Re =
`(\rho .U.x)/(\mu )`

Re =
`(1.21 * 5* 1)/(1.822* 10^(-5) )`

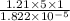
Re = 332052.6

Therefore the flow is laminar.

Hence boundary layer thickness is

δ =
`(5.x)/(√(Re))`

=
`(5* 1)/(√(332052.6))`

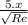
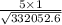
= 8.67 x
`10^(-3)` m

a). Boundary layer thickness at x = 1 is δ = 8.67 X
`10^(-3)` m

b). Given Re = 100000

Therefore the critical distance from the leading edge can be found by,

Re =
`(\rho .U.x)/(\mu )`

100000 =
`(1.21*5* x)/(1.822 *10^(-5))`

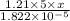
x = 0.3011 m

c). Given x = 3 m from the leading edge

The Reyonld no at x = 3 m from the leading edge

Re =
`(\rho .U.x)/(\mu )`

Re =
`(1.21 * 5* 3)/(1.822* 10^(-5) )`

Re = 996158.06

Therefore the flow is turbulent.

Therefore for a turbulent flow, boundary layer thickness is

δ =
`\frac{0.38* x}{Re^{(1)/(5)}}`

=
`\frac{0.38* 3}{996158.06^{(1)/(5)}}`

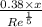
= 0.0719 m

d). Distance from the leading edge upto which the flow will be laminar,

Re =
`(\rho * U* x)/(\mu )`

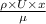
5 X
`10^(5)` =
`(1.21 * 5* x)/(1.822* 10^(-5))}`

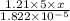
x = 1.505 m

We know that the force acting on the plate is

`F_(D)` =
`(1)/(2)* C_(D)* \rho * A* U^(2)`

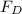and
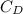`C_(D)` at x= 1.505 for a laminar flow is =
`(1.328)/(√(Re))`

=
`\frac{1.328}{\sqrt{5*10 ^(5)}}`

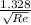
= 1.878 x
`10^(-3)`

Therefore,
`F_(D)` =
`(1)/(2)* C_(D)* \rho * A* U^(2)`

=
`(1)/(2)* 1.878* 10^(-3)* 1.21* (5* 1.505)* 5^(2)`

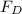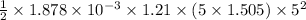
= 0.2137 N

e). The flow is turbulent at the end of the plate.

Re =
`(\rho * U* x)/(\mu )`

=
`(1.21 * 5* 6)/(1.822* 10^(-5) )`

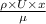
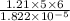
= 1992316

Therefore
`C_(D)` =
`\frac{0.072}{Re^{(1)/(5)}}`

=
`\frac{0.072}{1992316^{(1)/(5)}}`

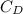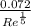
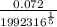
= 3.95 x
`10^(-3)`

Therefore
`F_(D)` =
`(1)/(2)* C_(D)* \rho* A* U^(2)`

=
`(1)/(2)* 3.95* 10^(-3)* 1.21* (5* 6)* 5^(2)`

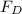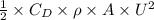
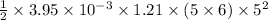
= 1.792 N