Answer:
by principal stress theory
t = 20.226
by total strain theory
t = 20.36
Step-by-step explanation:
given data
internal radius
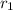 = 150 mm
= 150 mm
pressure p = 80 MPa
yield strength = 300 MPa
poisson's ratio = 0.3
a) by principal stress theory
thickness can be obtained as t
t =
![r_(1)\left [ ((\sigma _(y) +p)/(\sigma _(y) - 0.5p))^(1/3)-1 \right ]](https://img.qammunity.org/2020/formulas/engineering/college/9n05y29kq7ijttttwmjgau9szzwc6hq4hr.png)
t = = 150\left [ (\frac{300 +80}{300-0.5*80})^{1/3}-1 \right ]
t = 20.226
b) by total strain theory
m =
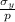
m =
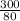 = 3.75
= 3.75
we know that
K =
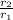
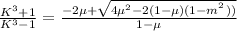
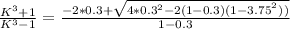
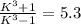
k = 1.13
1.13 =
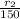
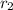 = 170.36 mm
= 170.36 mm
t =
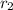 -
-
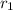
t = 170.36 - 150
t = 20.36