Question

A thick spherical pressure vessel of inner radius 150 mm is subjected to maximum an internal pressure of 80 MPa. Calculate its wall thickness based upon the (a) principal stress theory, and (b) total strain energy theory. Poisson's ratio = 0-30, yield strength 300 MPa.

Answer 1

by principal stress theory

t = 20.226

by total strain theory

t = 20.36

Step-by-step explanation:

given data

internal radius
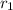`r_(1)` = 150 mm

pressure p = 80 MPa

yield strength = 300 MPa

poisson's ratio = 0.3

a) by principal stress theory

thickness can be obtained as t

t =
`r_(1)\left [ ((\sigma _(y) +p)/(\sigma _(y) - 0.5p))^(1/3)-1 \right ]`

t = = 150\left [ (\frac{300 +80}{300-0.5*80})^{1/3}-1 \right ]

t = 20.226

b) by total strain theory

m =
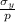
`(\sigma _(y))/(p)`

m =
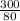`(300)/(80)` = 3.75

we know that

K =
`(r_(2))/(r_(1) )`

`(K^(3)+1)/(K^(3)-1)= \frac{-2\mu +\sqrt{4\mu^(2)-2(1-\mu)(1-m^{^(2)}))}}{1-\mu}`

`(K^(3)+1)/(K^(3)-1)= \frac{-2*0.3 +\sqrt{4*0.3^(2)-2(1-0.3)(1-3.75^{^(2)}))}}{1-0.3}`

`(K^(3)+1)/(K^(3)-1)= 5.3`

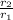
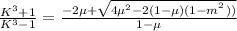
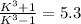
k = 1.13

1.13 =
`(r_(2))/(150 )`

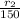
`r_(2)` = 170.36 mm

t =
`r_(2)`-
`r_(1)`

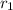
t = 170.36 - 150

t = 20.36