Question

A long homogeneous resistance wire of radius ro = 5 mm is being used to heat the air in a room by the passage of electric current. Heat is generated in the wire uniformly at a rate of g=5'107 W/m as a result of resistance heating. If the temperature of the outer surface of the wire remains at 180°C, determine the temperature at r = 2 mm after steady operation conditions are reached. Take the thermal conductivity of the wire to be k = 8 W/m x °C.

Answer 1

T = 212.8125°C

Step-by-step explanation:

Given

radius of the wire,
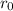`r_(0)` = 5 mm 0.005 m

heat generated, g = 5 x
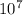`10^(7)` W/
`m^(3)`

outer surface temperature,
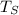`T_(S)` = 180°C

Thermal conductivity, k = 8 W / m-k

Now maximum temperature occurs at the center of the wire

that is at r=0,

Therefore,
`T_(o)=T_(S)+(g* r_(o)^(2))/(4* k)`

`T_(o)=180+(5* 10^(7)* 0.005^(2))/(4* 8)`

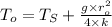
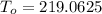`T_(o)=219.0625`°C

Therefore, temperature at r = 2 mm

`(T-T_(S))/(T_(O)-T_(S))= 1-\left ((r)/(r_(O))  \right )^(2)`

`(T-180)/(219.0625-180)= 1-\left ((2)/(5)  \right )^(2)`

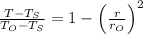
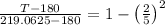
Therefore, T = 212.8125°C