Question

How much must you deposit each year into your retirement account starting now and continuing through year 10 if you want to be able to withdraw $75,000 per year forever, beginning 34 years from now? Assume the account earns interest at 10% per year.

Answer 1

This person would deposit $5,255.47 for ten years.

It will generated a value of $83758.62 which will coumpound interest for 23 years unit reach $750,000

After that, the person will withdraw 75,000 per year until his death

Step-by-step explanation:

Timeline:

for 10 year the person will do annual deposit.

24 years after that, wants to withdraw 75,000 forever AKA indefinite

`infinite \:anuity = (Principal)/(Rate) \\(75,000)/(0.10) = 750,000`

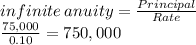
This is the future value needed for the person at the end of year 33 (Because at the beginning of year 34 It will withdraw 75,000)

This value will be the result of 23 years of interest of a lump sum

`Principal \timex (1+rate)^(time) = Amount`

`Principal \timex (1+0.10)^(23) = 750,000`

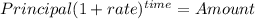
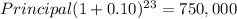
Principal = 83758.61835

This value will be the proceeds of the 10 years annuity

This is the future value of the annuity. This is the kicker of the investment. It starts from here.

`C * ((1+r)^(time) -1)/(rate) = FV\\`

`C * ((1+0.10)^(10) -1)/(0.10) = 83758.61835\\`

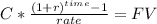
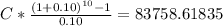
C = 5,255.467583