Question

0il with a relative density of 0,8 flows in a pipe of diameter 60 mm. A venturi meter having a throat diameter of 35 mm is installed in the pipeline. The pressure difference is measured with a mercury manometer. The levels of the manometer differ by 22 mm. The venturi meter has a discharge coefficient of 0,98. Calculate the flow rate of the oil.

Answer 1

the flow rate of the oil is 2.5 m³/s

Step-by-step explanation:

Given data

relative density (S) = 0.8

diameter (d1) = 60 mm = 0.06 m

diameter (d2) = 35 mm = 0.035 m

height (h) = 22 mm = 0.022 m

discharge coefficient (Cd) = 0.98

To find out

the flow rate of the oil

solution

we know the formula for rate of flow i.e.

flow rate = Cd a1 a2
`√(2 g n )` /
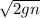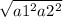`\sqrt{a1^(2) a2^(2) }` ...............1

here first we find area a1 and a2 i.e.

a1 = (
`\pi` /4 ) × d² = (
`\pi` /4 ) × 0.06² = 0.002827 m²

a2 = (
`\pi` /4 ) × d² = (
`\pi` /4 ) × 0.035² = 0.000962 m²

and now we find n = (density of mercury / density of oil) - 1 × h

n = ((13.56 / 0.8) - 1) × 0.022 = 0.3509

put all these value in equation 1

flow rate = Cd a1 a2
`√(2 g n )` /
`\sqrt{a1^(2) a2^(2) }`

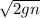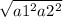
flow rate = 0.98× 0.002827× 0.000962
`√(2*9.81*0.3509)` /
`\sqrt{0.002827^(2) 0.000962^(2) }`

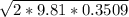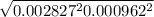
flow rate = 2.571386 m³/s