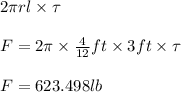Question

A cylinder 8 inches in diameter and 3 ft long is concentric with a pipe of 8.25 inches i.d. Between cylinder and pipe there is an oil film. What force is required to move the cylinder along the pipe at a constant velocity of 3 fps? The kinematic viscosity of the oil is 0.006 ft2 /s; the specific gravity is 0.92.

Answer 1

The force required to move the cylinder along the pipe can be calculated using the drag force formula. F = 6π(0.006)(1/3)(3) ≈ 0.113 ft-lbf

Step-by-step explanation:

To calculate the force required to move the cylinder along the pipe at a constant velocity, we need to consider the drag force acting on the cylinder.

The drag force can be calculated using the formula:

F = 6πηrv

Where F is the force, η is the viscosity of the oil, r is the radius of the cylinder, and v is the velocity of the cylinder.

In this case, the radius of the cylinder is half of the diameter, so the radius is 4 inches or 1/3 ft. The velocity is given as 3 fps.

Plugging in the values, we get:

F = 6π(0.006)(1/3)(3) ≈ 0.113 ft-lbf

Answer 2

Required force equals 623.498 lb

Step-by-step explanation:

We shall use newton's law of viscosity to calculate the shear force that acts on the cylinder

By Newton's law of viscosity we have

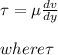`\tau =\mu (dv)/(dy)\\\\where \tau` is shear stress that acts on the internal surface

`\mu` is dynamic viscosity of the fluid

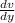`(dv)/(dy)` is the velocity gradient that exists across the flow

The dynamic viscosity is calculated as follows

`\mu =\rho \\u`

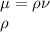`\mu =\rho \\u \\\rho` is density of the fluid

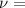`\\u =` kinematic viscosity of the fluid

By no slip boundary condition the fluid in contact with the stationary cylinder shall not have any velocity while as the fluid in contact with the moving cylinder shall have velocity equal to that of the cylinder itself. This implies a velocity gradient shall exist across the gap in between the cylinders.

Applying values of the quantities we can calculate shear stress as follows

The density of fluid is
`\rho=G* \rho_(w)`

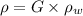
G = specific gravity of fluid

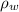`\rho_(w)`is density of water

`\tau =\rho \\u (dv)/(dy)\\\\\tau=62.42* 0.92* 0.006* (3)/((0.125inches)/(12inch))\\\\\tau=99.23lb/ft^(2)`

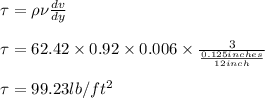
This pressure shall oppose the motion of the internal cylinder hence the force of opposition =
`F=\tau* Area`

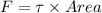
Using the area of internal cylinder we get total force

F=
`2\pi rl* \tau\\\\F=2\pi* (4)/(12)ft* 3ft* \tau\\\\ F=623.498lb`