Answer:16.096
Step-by-step explanation:
Given
mass of dog
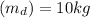
mass of boat
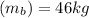
distance moved by dog relative to ground=
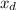
distance moved by boat relative to ground=
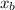
Distance moved by dog relative to boat=7.8m
There no net force on the system therefore centre of mass of system remains at its position
0=
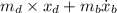
0=
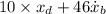
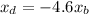
i.e. boat will move opposite to the direction of dog
Now
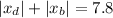
substituting
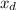 value
value



now the dog is 22.5-6.403=16.096m from shore