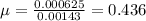Question

A cylindrical specimen of some metal alloy 11.2 mm (0.4409 in.) in diameter is stressed elastically in tension. A force of 14100 N (3170 lbf) produces a reduction in specimen diameter of 7 × 10-3 mm (2.756 × 10-4 in.). Compute Poisson's ratio for this material if its elastic modulus is 100 GPa (14.5 × 106 psi).

Answer 1

The Poisson's ratio for this material is 0.4370.

Step-by-step explanation:

Given that,

Diameter of metal = 11.2 mm

Force = 14100 N

Reduction diameter
`d=7*10^(-3)\ mm`

Elastic modulus = 100 GPa

We need to calculate the change in length

Using formula of modulus elasticity

`E=(FL)/(A\Delta L)`

The change in length is

`\Delta L=(FL)/(AE)`

`(\Delta L)/(L)=(14100)/(\pi*((11.2*10^(-3))^2)/(4)100*10^(9))`

`(\Delta L)/(L)=0.00143`

We need to calculate the Poisson's ratio

Using formula of Poisson's ratio

`\\u=(longitudinal\ strain)/(Transverse strain)`

`\\u=(-(\Delta d)/(d))/(-(\Delta L)/(L))`

Put the value into the formula

`\\u=((7*10^(-6))/(11.2*10^(-3)))/(0.00143)`

`\\u=0.4370`

Hence, The Poisson's ratio for this material is 0.4370.

Answer 2

μ = 0.436

Step-by-step explanation:

Given:

Change in diameter, ΔD = 7 × 10⁻³ mm

Original diameter, D = 11.2 mm = 11.2 × 10⁻³ m

Applied force, P = 14100 N

Cross-section area of the specimen, A =
`(\pi)/(4)D^2` =
`(\pi)/(4)(11.2* 10^(-3))^2`

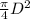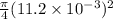
Now,

elongation due to tensile force is given as:

`\delta = (PL)/(AE)`

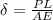
or

`(\delta)/(L) = (P)/(AE)`

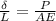
on substituting the values, we get

`(\delta)/(L) = (14100)/((\pi)/(4)(11.2* 10^(-3))^2*100* 10^9)`

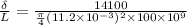
or

`(\delta)/(L) = 0.00143=\epsilon_x`

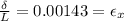
where,

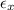`\epsilon_x` is the strain in the direction of force

Now,

`\epsilon_z=(\Delta D)/(D)=(7* 10^(-3))/(11.2)=0.000625`

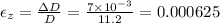
now, the poisson ratio, μ is given as:

`\mu=(\epsilon_z)/(\epsilon_x)`

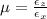
on substituting the values we get,

`\mu=(0.000625)/(0.00143)=0.436`