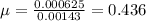Answer:
μ = 0.436
Step-by-step explanation:
Given:
Change in diameter, ΔD = 7 × 10⁻³ mm
Original diameter, D = 11.2 mm = 11.2 × 10⁻³ m
Applied force, P = 14100 N
Cross-section area of the specimen, A =
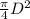 =
=
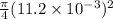
Now,
elongation due to tensile force is given as:
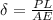
or
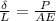
on substituting the values, we get
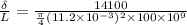
or
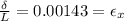
where,
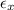 is the strain in the direction of force
is the strain in the direction of force
Now,
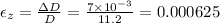
now, the poisson ratio, μ is given as:
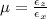
on substituting the values we get,