Answer:
Explanation:
If each day equal chance then p = Prob that a person is borne on a particular day = 1/365
Each person is independent of the other and there are two outcomes either borne in July or not
p = prob for one person not borne in July = (365-31)/365 = 334/365
a)Hence prob that no one from n people borne in July =
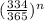
b) p = prob of any one borne in July or Aug =
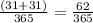 =0.1698
=0.1698
X- no of people borne in July or Aug
n =15
P(X>=2) =
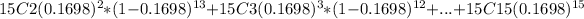
=0.7505