Answer:
The change in length is 3.4 mm.
Step-by-step explanation:
Given that,
Length = 4 m
Diameter = 2.3 cm
Load = 70 kN
Modulus of elasticity = 200 GPa
We need to calculate the change in length
Using formula of modulus of elasticity
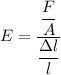
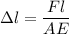
Where, F = force
A = area
L = length
E = modulus elasticity
Put the value into the formula
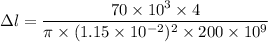
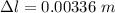
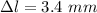
Hence, The change in length is 3.4 mm.