Answer:
Explanation:
By definition of Laplace transform we have
L{f(t)} =
![L{{f(t)}}=\int_(0)^(\infty )e^(-st)f(t)dt\\\\Given\\f(t)=7t^(3)\\\\\therefore L[7t^(3)]=\int_(0)^(\infty )e^(-st)7t^(3)dt\\\\](https://img.qammunity.org/2020/formulas/mathematics/college/let16i64z7frf73u7e966wr6x82da1u6qc.png)
Now to solve the integral on the right hand side we shall use Integration by parts Taking
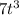 as first function thus we have
as first function thus we have
![\int_(0)^(\infty )e^(-st)7t^(3)dt=7\int_(0)^(\infty )e^(-st)t^(3)dt\\\\= [t^3\int e^(-st) ]_(0)^(\infty)-\int_(0)^(\infty )[(3t^2)\int e^(-st)dt]dt\\\\=0-\int_(0)^(\infty )(3t^(2))/(-s)e^(-st)dt\\\\=\int_(0)^(\infty )(3t^(2))/(s)e^(-st)dt\\\\](https://img.qammunity.org/2020/formulas/mathematics/college/sf9s686unbfc24ns3ucoybddp7py2umyyy.png)
Again repeating the same procedure we get
![=0-\int_(0)^(\infty )(3t^(2))/(-s)e^(-st)dt\\\\=\int_(0)^(\infty )(3t^(2))/(s)e^(-st)dt\\\\\int_(0)^(\infty )(3t^(2))/(s)e^(-st)dt= (3)/(s)[t^2\int e^(-st) ]_(0)^(\infty)-\int_(0)^(\infty )[(t^2)\int e^(-st)dt]dt\\\\=(3)/(s)[0-\int_(0)^(\infty )(2t^(1))/(-s)e^(-st)dt]\\\\=(3* 2)/(s^(2))[\int_(0)^(\infty )te^(-st)dt]\\\\](https://img.qammunity.org/2020/formulas/mathematics/college/6136mfb83xllh0iz42c3brs60y730q5kqb.png)
Again repeating the same procedure we get
![(3* 2)/(s^2)[\int_(0)^(\infty )te^(-st)dt]= (3* 2)/(s^(2))[t\int e^(-st) ]_(0)^(\infty)-\int_(0)^(\infty )[(t)\int e^(-st)dt]dt\\\\=(3* 2)/(s^2)[0-\int_(0)^(\infty )(1)/(-s)e^(-st)dt]\\\\=(3* 2)/(s^(3))[\int_(0)^(\infty )e^(-st)dt]\\\\](https://img.qammunity.org/2020/formulas/mathematics/college/uupevdrd73okvzubiqvbbxopfgbrzed6au.png)
Now solving this integral we have
![\int_(0)^(\infty )e^(-st)dt=(1)/(-s)[(1)/(e^\infty )-(1)/(1)]\\\\\int_(0)^(\infty )e^(-st)dt=(1)/(s)](https://img.qammunity.org/2020/formulas/mathematics/college/k00tpjpifvdybap4a9m5552yxlvyo5fn4c.png)
Thus we have
![L[7t^(3)]=(7* 3* 2)/(s^4)](https://img.qammunity.org/2020/formulas/mathematics/college/n8nz7bamw6dshwlh9zes4zj7qu7stqxvdx.png)
where s is any complex parameter