Question

What is the Laplace Transform of 7t^3 using the definition (and not the shortcut method)

Answer 1

Explanation:

By definition of Laplace transform we have

L{f(t)} =
`L{{f(t)}}=\int_(0)^(\infty )e^(-st)f(t)dt\\\\Given\\f(t)=7t^(3)\\\\\therefore L[7t^(3)]=\int_(0)^(\infty )e^(-st)7t^(3)dt\\\\`

Now to solve the integral on the right hand side we shall use Integration by parts Taking
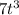`7t^(3)` as first function thus we have

`\int_(0)^(\infty )e^(-st)7t^(3)dt=7\int_(0)^(\infty )e^(-st)t^(3)dt\\\\= [t^3\int e^(-st) ]_(0)^(\infty)-\int_(0)^(\infty )[(3t^2)\int e^(-st)dt]dt\\\\=0-\int_(0)^(\infty )(3t^(2))/(-s)e^(-st)dt\\\\=\int_(0)^(\infty )(3t^(2))/(s)e^(-st)dt\\\\`

Again repeating the same procedure we get

`=0-\int_(0)^(\infty )(3t^(2))/(-s)e^(-st)dt\\\\=\int_(0)^(\infty )(3t^(2))/(s)e^(-st)dt\\\\\int_(0)^(\infty )(3t^(2))/(s)e^(-st)dt= (3)/(s)[t^2\int e^(-st) ]_(0)^(\infty)-\int_(0)^(\infty )[(t^2)\int e^(-st)dt]dt\\\\=(3)/(s)[0-\int_(0)^(\infty )(2t^(1))/(-s)e^(-st)dt]\\\\=(3* 2)/(s^(2))[\int_(0)^(\infty )te^(-st)dt]\\\\`

Again repeating the same procedure we get

`(3* 2)/(s^2)[\int_(0)^(\infty )te^(-st)dt]= (3* 2)/(s^(2))[t\int e^(-st) ]_(0)^(\infty)-\int_(0)^(\infty )[(t)\int e^(-st)dt]dt\\\\=(3* 2)/(s^2)[0-\int_(0)^(\infty )(1)/(-s)e^(-st)dt]\\\\=(3* 2)/(s^(3))[\int_(0)^(\infty )e^(-st)dt]\\\\`

Now solving this integral we have

`\int_(0)^(\infty )e^(-st)dt=(1)/(-s)[(1)/(e^\infty )-(1)/(1)]\\\\\int_(0)^(\infty )e^(-st)dt=(1)/(s)`

Thus we have

`L[7t^(3)]=(7* 3* 2)/(s^4)`

where s is any complex parameter