Question

A fire hose has an inside diameter of 6.40 cm. Suppose such a hose carries a flow of 40.0 L/s starting at a gauge pressure of 1.62 x 106 N/m2. Calculate the Reynolds numbers for flow in the fire hose.

Answer 1

The Reynolds numbers for flow in the fire hose.

Step-by-step explanation:

Given that,

Diameter = 6.40 cm

Rate of flow = 40.0 L/s

Pressure
`P=1.62*10^(6)\ N/m^2`

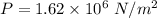
We need to calculate the Reynolds numbers for flow in the fire hose

Using formula of rate of flow

`Q=Av`

`v=(Q)/(A)`

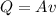
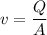
Where, Q = rate of flow

A = area of cross section

Put the value into the formula

`v=(40.0*10^(-3))/(3.14*(3.2*10^(-2))^2)`

`v=12.44\ m/s`

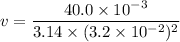
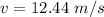
We need to calculate the Reynolds number

Using formula of the Reynolds number

`n_(R)=(2\rho* v* r)/(\eta)`

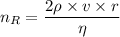
Where,
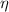`\eta` =viscosity of fluid

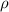`\rho` =density of fluid

Put the value into the formula

`n_(R)=(2*100*12.44*3.2*10^(-2))/(1.002*10^(-3))`

`n_(R)=7.945*10^(5)`

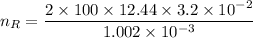
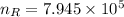
Hence, The Reynolds numbers for flow in the fire hose.