Answer:
Part a)
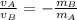
Part b)

Step-by-step explanation:
Part a)
As we know that initially the two blocks are connected by a spring and initially stretched by some amount
Since the two blocks are at rest initially so its initial momentum is zero
since there is no external force on this system so final momentum is also zero
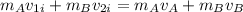
now for initial position the speed is zero
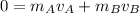
now we have
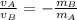
Part b)
now for ratio of kinetic energy we know that the relation between kinetic energy and momentum is given as
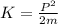
now for the ratio of energy we have
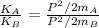
since we know that momentum of two blocks are equal in magnitude so we have
now we have
