Question

Two particles travel along the space curves r1(t) = t, t2, t3 r2(t) = 1 + 2t, 1 + 6t, 1 + 14t . Find the points at which their paths intersect. (If an answer does not exist, enter DNE.)

Answer 1

DNE

Explanation:

Given that two particles travel along the space curves

`r_1(t) = (t, t^2, t^3)\\ r_2(t) = (1 + 2t, 1 + 6t, 1 + 14t )`

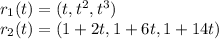
To find the points of intersection:

At points of intersection both coordinates should be equal.

i.e. r1 =r2

Equate corresponding coordinates

`t=1+2t\\t^2=1+6t\\t^3=1+14t`

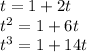
I equation gives t =-1

Substitute in II equation to get
`t^2 = -5`

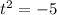
i.e. t cannot be real

Hence no point of intersection

DNE