Answer : The height of the unit cell is,

Explanation : Given,
Density of zinc =
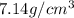
Atomic radius =
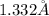
Atomic weight of zinc = 65.37 g/mole
As we know that, zinc has haxagonal close packed crystal structure. The number of atoms in unit cell of HCP is, 6.
Formula used for density :
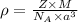 .............(1)
.............(1)
where,
 = density of zinc
= density of zinc
Z = number of atom in unit cell = 6 atoms/unit cell (for HCP)
M = atomic mass
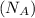 = Avogadro's number =
= Avogadro's number =
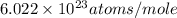
a = edge length of unit cell
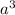 = volume of unit cell
= volume of unit cell
Now put all the values in above formula (1), we get
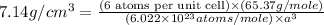
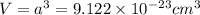
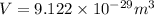
Now we have to calculate the height of the unit cell.
Formula used :
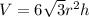
where,
V = volume of unit cell
r = atomic radius =
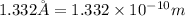
conversion used :
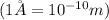
h = height of the unit cell
Now put all the given values in this formula, we get:
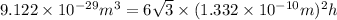
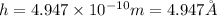
Therefore, the height of the unit cell is,
