Question

A jet turbine rotates at a velocity of 7,500 rpm. Calculate the stress acting on the turbine blades if the turbine disc radius is 70 cm and the cross-sectional area is 15 cm2. Take the length to be 10 cm and the alloy density to be 8.5 g/cm3.

Answer 1

stress = 366515913.6 Pa

Step-by-step explanation:

given data:

density of alloy = 8.5 g/cm^3 = 8500 kg/m^3

length turbine blade = 10 cm = 0.1 m

cross sectional area = 15 cm^2 = 15*10^-4 m^2

disc radius = 70 cm = 0.7 m

angular velocity = 7500 rpm = 7500/60 rotation per sec

we know that

stress = force/ area

force = m*a

where a_{c} is centripetal acceleration =

`a_(c) =r*\omega ^(2)= r*(2*\pi*\omega)^(2)`

=
`0.70*(2*\pi*(7500)/(60))^(2)`

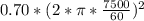
= 431795.19 m/s^2

mass =
`\rho* V`

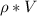
Volume = area* length = 15*10^{-5} m^3

`mass = m = \rho*V = 8500*15*10^(-5) kg`

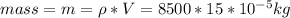
force = m*a_{c}

`=8500*15*10^(-5)*0.70*(2*\pi*(7500)/(60))^(2)`

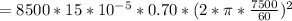
force = 549773.87 N

stress = force/ area

=
`(549773.87)/(15*10^(-5))`

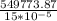
stress = 366515913.6 Pa