Question

pH measurements of a chemical solutions have mean 6.8 with standard deviation 0.02. Assuming all pH measurements of this solution have a nearly symmetric/bell-curve distribution. Find the percent (%) of pH measurements reading below 6.74 OR above 6.76.

Answer 1

Answer: 2.14 %

Explanation:

Given : pH measurements of a chemical solutions have

Mean :
`\mu=6.8`

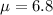
Standard deviation :
`\sigma=0.02`

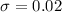
Let X be the pH reading of a randomly selected customer chemical solution.

We assume pH measurements of this solution have a nearly symmetric/bell-curve distribution (i.e. normal distribution).

The z-score for the normal distribution is given by :-

`z=(x-\mu)/(\sigma)`

For x = 6.74

`z=(6.74-6.8)/(0.02)=-3`

For x = 6.76

`z=(6.76-6.8)/(0.02)=-2`

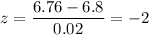
The p-value =
`P(6.74<x<6,76)=P(-3<z<-2)`

`P(z<-2)-P(z<-3)=0.0227501- 0.0013499=0.0214002\approx0.0214`

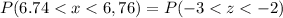
In percent,
`0.0214*=2.14\%`

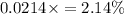
Hence, the percent of pH measurements reading below 6.74 OR above 6.76 = 2.14%