Question

It is desired to create a particle of mass 7920 MeV/c^2 in a head-on collision between a proton and an antiproton (each having a mass of 938.3 MeV/c^2) traveling at the same speed. What peed is necessary for this to occur?

Answer 1

`v=0.9714c`

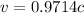
Step-by-step explanation:

The kinetic energy possessed by particles will be

`K.E=(1)/(2)Mc^2`

where,

M is the mass of the particle (7920938.3 MeV/c²)

c is the speed of the light

Also,

energy of the proton particle =
`\frac{m_pc^2}{\sqrt{1-(v^2)/(c^2)}}`

where,

v is the velocity

m_p is the mass of the proton (938.3 MeV/c²)

since the energy is equal

thus,

`\frac{m_pc^2}{\sqrt{1-(v^2)/(c^2)}}=(1)/(2)Mc^2`

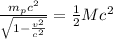
or

`1-(v^2)/(c^2)=[(2m_p)/(M)]^2`

substituting the values in the above equation, we get

`1-(v^2)/(c^2)=[(2* 938.3 )/(7920)]^2`

or

`v=0.9714c`

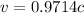
Hence, the speed necessary for the specified condition to occur is 0.9714 times the speed of the light