Answer:
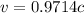
Step-by-step explanation:
The kinetic energy possessed by particles will be
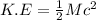
where,
M is the mass of the particle (7920938.3 MeV/c²)
c is the speed of the light
Also,
energy of the proton particle =
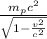
where,
v is the velocity
m_p is the mass of the proton (938.3 MeV/c²)
since the energy is equal
thus,
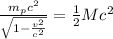
or
![1-(v^2)/(c^2)=[(2m_p)/(M)]^2](https://img.qammunity.org/2020/formulas/physics/college/acpj8h924btvfcm5iatnhby6g57h29fps0.png)
substituting the values in the above equation, we get
![1-(v^2)/(c^2)=[(2* 938.3 )/(7920)]^2](https://img.qammunity.org/2020/formulas/physics/college/7cwovdwzi0y34yetwnmook6xnbgz3ripwr.png)
or
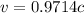
Hence, the speed necessary for the specified condition to occur is 0.9714 times the speed of the light