Question

How many edges must be removed from the wheel graph W6 in order to create a spanning tree for the graph?

a) 5
b) 6
c) 7
d) The graph does not have a spanning tree.

Answer 1

The correct option is A.

Explanation:

If a graph is formed by connecting a single universal vertex to all vertices of a cycle, then it is known as wheel graph.

W₆ means wheel graph having 6 vertices as shown in the below figure.

Total number of edges in a wheel graph is 2(n-1), where n is number of vertices. So, the number of edges in W₆ is

`2(6-1)=10`

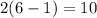
In a spanning tree all the vertices covered with minimum possible number of edges. Total number of edges in a spanning tree is (n-1).

Total number of edges in a spanning tree which has 6 vertices is

`6-1=5`

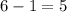
The number of edges we need to remove is

`10-5=5`

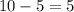
Therefore the correct option is A.