Answer:
The two intersections are (3/2 , 5/4) and (4,0).
I put two ways to do it. You can pick your favorite of these are try another route if you like.
Explanation:
The system is:
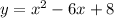
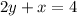 .
.
I don't know how good at factoring you are but the top equation consists of polynomial expression that has a factor of (x-4). I see that if I solve 2y+x=4 for 2y I get 2y=-x+4 which is the opposite of (x-4) so -2y=x-4.
So anyways, factoring x^2-6x+8=(x-4)(x-2) because -4+(-2)=-6 while -4(-2)=8.
This is the system I'm looking at right now:
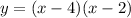
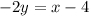
I'm going to put -2y in for (x-4) in the first equation:
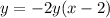
So one solution will occur when y is 0.
Now assume y is not 0 and divide both sides by y:
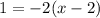
Distribute:
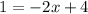
Subtract 4 on both sides:
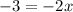
Divide both sides by -2:
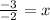
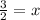
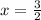
Now let's go back to one of the original equations:
2y=-x+4
Divide both sides by 2:
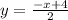
Plug in 3/2 for x:
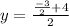
Multiply top and bottom by 2:
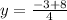
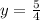
So one solution is at (3/2 , 5/4).
The other solution happened at y=0:
2y=-x+4
Plug in 0 for y:
2(0)=-x+4
0=-x+4
Add x on both sides:
x=4
So the other point of intersection is (4,0).
-------------------------------------------------------
The two intersections are (3/2 , 5/4) and (4,0).
Now if you don't like that way:
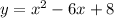
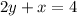
Replace y in bottom equation with (x^2-6x+8):
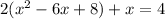
Distribute:

Subtract 4 on both sides:
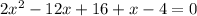
Combine like terms:
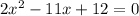
Compare this to

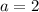
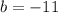

The quadratic formula is
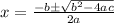
{Plug in our numbers:
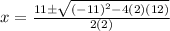
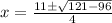
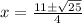
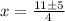
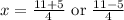
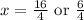
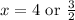
Using 2y+x=4 let's find the correspond y-coordinates.
If x=4:
2y+4=4
Subtract 4 on both sides:
2y=0
Divide both sides by 2:
y=0
So we have (4,0) is a point of intersection.
If x=3/2
2y+(3/2)=4
Subtract (3/2) on both sides:
2y=4-(3/2)
2y=5/2
Divide 2 on both sides:
y=5/4
The other intersection is (3/2 , 5/4).