Answer:
m∠P=70°, m∠T=20°, m∠SKP=40°, and m∠MKT=70°.
Explanation:
Given information: △PST, m∠S=90°, M∈ segment PT, segment PM ≅ MT, MK ⊥ PT, m∠SPK/m∠KPM = 5/2.
Let the measure of m∠SPK and ∠KPM are 5x° and 2x° respectively.
In triangle PKM and TKM,
 (Common side)
(Common side)
 (MK ⊥ PT)
(MK ⊥ PT)
 (Given)
(Given)
By SAS postulate,
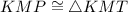
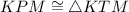 (CPCTC)
(CPCTC)
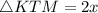
According to angle sum property, the sum of interior angles of a triangle is 180°.
Use angle sum property in triangle SPT,
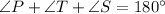
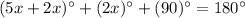

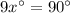
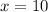
The value of x is 10.
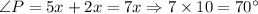
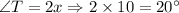
Therefore, m∠P=70° and m∠T=20°.
Use angle sum property in triangle SPK.
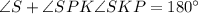
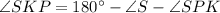

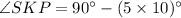
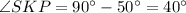
Therefore the measure of ∠SKP is 40°.
Use angle sum property in triangle MKT.
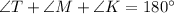
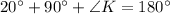

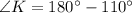
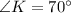
Therefore, the measure of ∠MKT is 70°.