Question

How can I solve this.

Given: △PST, m∠S=90°, M∈ segment PT,
segment PM ≅ MT,
MK ⊥ PT
m∠SPK/m∠KPM = 5/2

Find: m∠P, m∠T, m∠SKP, and m∠MKT

Answer 1

I have that question too for my school work. Can u help me Pls?

Answer 2

m∠P=70°, m∠T=20°, m∠SKP=40°, and m∠MKT=70°.

Explanation:

Given information: △PST, m∠S=90°, M∈ segment PT, segment PM ≅ MT, MK ⊥ PT, m∠SPK/m∠KPM = 5/2.

Let the measure of m∠SPK and ∠KPM are 5x° and 2x° respectively.

In triangle PKM and TKM,

`KM\cong KM` (Common side)

`\anlge KMP\cong \angle KMT` (MK ⊥ PT)

`PM\cong MT` (Given)

By SAS postulate,

`\trianlge KMP\cong \triangle KMT`

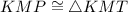
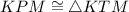`\anlge KPM\cong \triangle KTM` (CPCTC)

`\triangle KTM=2x`

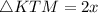
According to angle sum property, the sum of interior angles of a triangle is 180°.

Use angle sum property in triangle SPT,

`\angle P+\angle T+\angle S=180^(\circ)`

`(5x+2x)^(\circ)+(2x)^(\circ)+(90)^(\circ)=180^(\circ)`

`9x^(\circ)=180^(\circ)-90^(\circ)`

`9x^(\circ)=90^(\circ)`

`x=10`

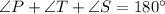
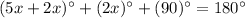
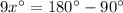
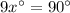
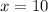
The value of x is 10.

`\angle P=5x+2x=7x\Rightarrow 7* 10=70^(\circ)`

`\angle T=2x\Rightarrow 2* 10=20^(\circ)`

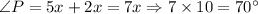
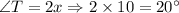
Therefore, m∠P=70° and m∠T=20°.

Use angle sum property in triangle SPK.

`\angle S+\angle SPK\angle SKP=180^(\circ)`

`\angle SKP=180^(\circ)-\angle S-\angle SPK`

`\angle SKP=180^(\circ)-90^(\circ)-(5x)^(\circ)`

`\angle SKP=90^(\circ)-(5* 10)^(\circ)`

`\angle SKP=90^(\circ)-50^(\circ)=40^(\circ)`

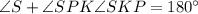
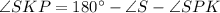
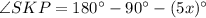
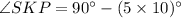
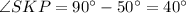
Therefore the measure of ∠SKP is 40°.

Use angle sum property in triangle MKT.

`\angle T+\angle M+\angle K=180^(\circ)`

`20^(\circ)+90^(\circ)+\angle K=180^(\circ)`

`110^(\circ)+\angle K=180^(\circ)`

`\angle K=180^(\circ)-110^(\circ)`

`\angle K=70^(\circ)`

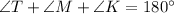
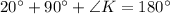
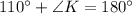
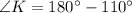
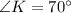
Therefore, the measure of ∠MKT is 70°.