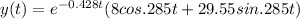Question

Find y as a function of t if 49y" + 42y' + 13y = 0, y(0) = 8, y'(0) = 5. y(t) =

Answer 1

`y(t)=e^(.428 t)(8cos\0.285 t+29.55sin\0.285t)`

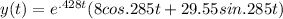
Explanation:

Given:

49y''+42y'+13y=0 ,y(0)=8,y'(0)=5

Lets take a y''+by'+c=0 is a differential equation.

So auxiliary equation will be

`a m^2+b m+c=0`

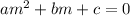
So according to given problem our auxiliary equation will be

`49 m^2+42 m+13=0`

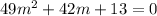
Then the roots of above equation

`m=(-b\pm √(b^2-4ac))/(2a)`

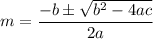
But D in the above question is negative so the roots of equation will be imaginary (
`D=b^2-4ac`).

By solving m= -0.428+0.285i , -0.428-0.285i,

m=
`\alpha \pm \beta`

So
`y(t)=e^(\alpha t)(C_1cos\beta t+C_2sin\beta t)`

`y(t)=e^(-0.428 t)(C_1cos\0.285 t+C_2sin\0.285t)`

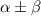
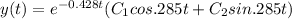
So now by using giving condition we will find

`C_1=8 ,C_2= 29.55`

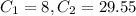
So
`y(t)=e^(-0.428 t)(8cos\0.285 t+29.55sin\0.285t)`