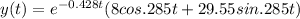Answer:
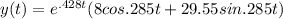
Explanation:
Given:
49y''+42y'+13y=0 ,y(0)=8,y'(0)=5
Lets take a y''+by'+c=0 is a differential equation.
So auxiliary equation will be
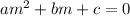
So according to given problem our auxiliary equation will be
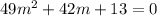
Then the roots of above equation
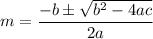
But D in the above question is negative so the roots of equation will be imaginary (
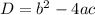 ).
).
By solving m= -0.428+0.285i , -0.428-0.285i,
m=
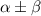
So
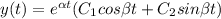
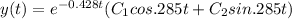
So now by using giving condition we will find
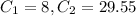
So