Answer:
The length of the rectangular key is 0.4244 m
Step-by-step explanation:
Given that,
Power = 7.46 kW
Speed = 1200 rpm
Shearing stress of shaft = 30 MPa
Mini shearing stress of key = 240 MPa
We need to calculate the torque
Using formula of power
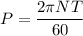
Where, P = power
N = number of turns
Put the value into the formula
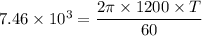
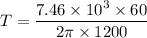
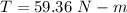
We need to calculate the distance
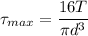

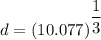
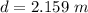
Width of key is one fourth of the shaft diameter
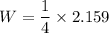

The shear stress induced in key
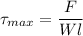
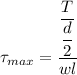

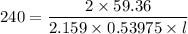
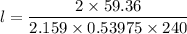

Hence, The length of the rectangular key is 0.4244 m