Answer:
(2,4) and (-2,-4).
Explanation:
We consider the system
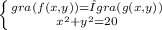
where g(x,y)=
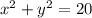
gra(f(x,y))= (4,8)
gra(g(x,y))=(2x,2y)
So,
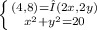
We have then that 4=2λx and 8=2λy. Dividing the second equation by 2 at both sides we obtain 4=λy. So, 4=2λx and 4=λy, we equalize both equations:
2λx=λy ⇔ 2x=y.
We replace that y value in the constraint equation:
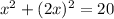
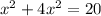
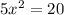
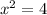
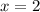 and
and

With this two x values and the y equation y= 2x we can obtain the extremes: (2,4) and (-2,-4).