Question

Determine if the given mapping phi is a homomorphism on the given groups. If so, identify its kernel and whether or not the mapping is 1-1 or onto. (a) G is a group, phi: G rightarrow G is defined by phi (a) = a^-1 for a elementof G. (b) G is an abelian group, n > 1 is a fixed integer, and phi: G rightarrow G is defined by phi (a) = a^n for a elementof G. (c) phi: C^x rightarrow R^x with phi (a) = |a|. (d) phi: R rightarrow C^x with phi (x) = cos x + i sin x.

Answer 1

(a) No. (b)Yes. (c)Yes. (d)Yes.

Explanation:

(a) If
`\phi: G \longrightarrow G` is an homomorphism, then it must hold

that
`b^(-1)a^(-1)=(ab)^(-1)=\phi(ab)=\phi(a)\phi(b)=a^(-1)b^(-1)`,

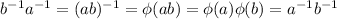but the last statement is true if and only if G is abelian.

(b) Since G is abelian, it holds that

`\phi(a)\phi(b)=a^nb^n=(ab)^(n)=\phi(ab)`

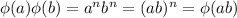
which tells us that
`\phi` is a homorphism. The kernel of
`\phi`

is the set of elements g in G such that
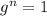`g^(n)=1`. However,

`\phi` is not necessarily 1-1 or onto, if
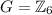`G=\mathbb{Z}_6` and

n=3, we have

`kern(\phi)=\{0,2,4\} \quad \text{and} \quad\\\\Im(\phi)=\{0,3\}`

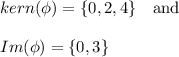
(c) If
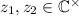`z_1,z_2 \in \mathbb{C}^(*)` remeber that

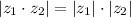`|z_1 \cdot z_2|=|z_1|\cdot|z_2|`, which tells us that
`\phi` is a

homomorphism. In this case

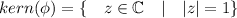`kern(\phi)=\{\quad z\in\mathbb{C} \quad | \quad |z|=1 \}`, if we write a

complex number as
`z=x+iy`, then
`|z|=x^2+y^2`, which tells

us that
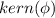`kern(\phi)` is the unit circle. Moreover, since

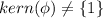`kern(\phi) \\eq \{1\}` the mapping is not 1-1, also if we take a negative

real number, it is not in the image of
`\phi`, which tells us that

`\phi` is not surjective.

(d) Remember that
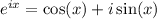`e^(ix)=\cos(x)+i\sin(x)`, using this, it holds that

`\phi(x+y)=e^(i(x+y))=e^(ix)e^(iy)=\phi(x)\phi(x)`

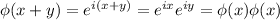
which tells us that
`\phi` is a homomorphism. By computing we see

that
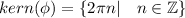`kern(\phi)=\{2 \pi n| \quad n \in \mathbb{Z} \}` and

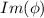`Im(\phi)` is the unit circle, hence
`\phi` is neither injective nor

surjective.