Question

Determine the discriminant for the quadratic equation -3 = x^2+4x+1 . Based on the discriminant value, how many real number solutions does the equation have?

Answer 1

the correct choice is B

Explanation:

Answer 2

1 real

Explanation:

The discriminant is:

`b^2-4ac`

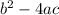
which comes from the quadratic formula.

The rules are:

If the discriminant is > 0, there are 2 real solutions

If the discriminant is = 0, there is 1 real solution

If the discriminant is < 0, there are 2 imaginary solutions

(there are 2 other situations involving square roots, but these are the most basic ones in Algebra 2 books when you study quadratics)

First, we have to get that quadratic in standard form, which means getting everything on one side of the equals sign and setting it equal to 0:

`x^2+4x+4 = 0`

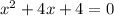
where a = 1, b = 4, c = 4

Filling in the discriminant:

`4^2-4(1)(4)`

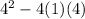
gives us

16 - 16 = 0

Therefore, our quadratic has one real solution. Factor it and see if you'd like, to prove that it is true.