Answer:
First option:
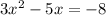
Second option:
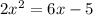
Fourth option:
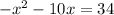
Explanation:
Rewrite each equation in the form
 and then use the Discriminant formula for each equation. This is:
and then use the Discriminant formula for each equation. This is:

1) For
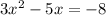 :
:
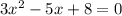
Then:

Since
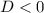 this equation has no real solutions, but has two complex solutions.
this equation has no real solutions, but has two complex solutions.
2) For
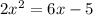 :
:
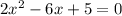
Then:
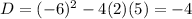
Since
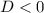 this equation has no real solutions, but has two complex solutions.
this equation has no real solutions, but has two complex solutions.
3) For
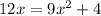 :
:
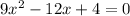
Then:

Since
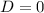 this equation has one real solution.
this equation has one real solution.
4) For
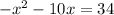 :
:
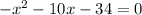
Then:
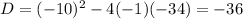
Since
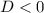 , this equation has no real solutions, but has two complex solutions.
, this equation has no real solutions, but has two complex solutions.