Answer:
Explanation:
From the given information:
The null hypothesis: all three brands are equally likely to their expected value
The alternative hypothesis: preferences exist among the three brands i.e. at least one is different from the expected value.
The expected frequency =
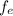
The observed frequency =
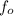
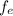
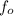
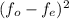

37 30 49.00 1.633
21 30 81.00 2.700
32 30 4.00 0.133
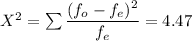
Degree of freedom =

= 3 -1
= 2
At ∝ = 0.05 and df = 2
The critical value

Decision rule:
Since the calculated chi-square is less than the critical value, we do not reject the null hypothesis.
Thus, the null is retained with a calculated chi-square value of 4.47 and a critical chi-square value of 5.99.