Question

A bartender slides a beer mug at 1.6 m/s towards a customer at the end of a frictionless bar that is 1.1 m tall. The customer makes a grab for the mug and misses, and the mug sails off the end of the bar.

(a) How far away from the end of the bar does the mug hit the floor?
m

(b) What are the speed and direction of the mug at impact?

speed m/s
direction ° below the horizontal

Answer 1

(a) x = 0.758 m

(b) v = 4.9 m/s, α = 70.97° below the horizontal

Step-by-step explanation:

The movement is semi-parabolic because the initial velocity is horizontal.

The equations of semiparabolic motion are:

x movement : uniform line movement

x= vx*t Equation (1)

Where:

x: horizontal position in meters (m)

t : time (s)

vx: horizontal velocity in m/s

y movement: free fall motion

y = (1/2)g*t² Equation (2)

vy= g*t Equation (3)

Where:

y: vertical position in meters (m)

t : time in seconds (s)

vy: vertical velocity in m/s

g: acceleration due to gravity in m/s²

Data

Vx = 1.6 m/s

y = 1.1 m

g = 9.8 m/s²

Time it takes for the beer mug to hit the floor

We replace in the formula (2)

y = (1/2)g*t²

1.1 = (1/2) (9.8)*t²

t² =(2*1.1)/ (9.8)

`t = \sqrt{(2*1.1)/(9.8) }`

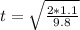
t= 0.474 s

Horizontal distance the mug reaches

We replace vx= 1.6 m/s and t= 0.474 s in the formula (1):

x = vx*t = (1.6) *(0.474)

x = 0.758 m

Speed (v) and direction (α) of the mug at impact :

In the Equation (3): vy= g*t = 9.8* 0.474 = 4.645 m/s (downward)

`v = \sqrt{v_(x)^(2)+v_(y)^(2)  }`

`v = \sqrt{1.6^(2)+4.645^(2)  }`

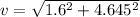
v = 4.9 m/s

`\alpha = tan^(-1) ((v_(y) )/(v_(x) ) )`

`\alpha = tan^(-1) ((-4.645 )/(1.6) )`

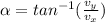
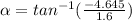
α = - 70.97°

α = below the horizontal

Answer 2

(a): the mug hits the floor 0.752m away from the end of the bar.

(b): the speed of the mug at impact are:

V= 4.87 m/s

direction= 70.82º below the horizontal.

Step-by-step explanation:

Vx= 1.6 m/s

Vy=?

h= 1.1 m

g= 9.8 m/s²

t is the fall time

`t=\sqrt{(2*h)/(g) }`

t=0.47 sec

Vy= g*t

Vy= 4.6 m/s

`V=\sqrt{Vx^(2) +Vy^(2)`

V= 4.87 m/s

α= tan⁻¹(Vy/Vx)

α= -70.82º