Answer with explanation:
The vertices of Quadrilateral ABCD are ,A(−5,7), B(6,−3), C(10,2), and D(−1,12).
Distance formula between two points (a,b) and (c,d), is given by
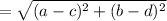
![AB=√([-5-6]^2+[7-(-3)]^2)\\\\AB=√(121+100)\\\\AB=√(221)\\\\BC=√([10-6]^2+(2+3)^2)\\\\BC=√(16+25)\\\\BC=√(41)\\\\CD=√([10+1]^2+[2-12]^2)\\\\CD=√(121+100)\\\\CD=√(221)\\\\DA=√([-1+5]^2+[12-7]^2)\\\\DA=√(16+25)\\\\DA=√(41)\\\\AC=√([10+5]^2+[2-7]^2)\\\\AC=√(225+25)\\\\AC=√(250)\\\\BD=√([6+1]^2+[-3-12]^2])\\\\BD=√(49+225)\\\\BD=√(274)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/xk2yifygpvn95ppuzkakijvkhyljopauae.png)
Opposite side of Quadrilateral[AB=CD, AD=BC] is equal, but Diagonals are not equal.
So, it is a Parallelogram.