Answer:
0.0488%
Explanation:
Here we have the probability of different independent events, which means that none of the previous ones affect the next. For this kind of events, the probability 'P' that a series of events occur is the multiplication of the probability of each singular event.
p1: Probability that an H be obtained: 50% (is always 50% because it is independent of the previous results)
P: The probability that H be obtained all of the 10 times. This is the complementary probability to E:(a T comes up at least once).
By the first definition given
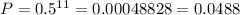
The complementary probability 'P' is the probability that 'E' does not happen, so the probability that E happen is:

The last makes sense if we think about the fact that for the experiment there are just two possibilities, 'E' happen, or 'E' does not happen. Then,
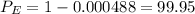 %
%