Question

(b) Prove that there is a unique integer n for which 2n^2-3n-2=0.

Answer 1

The only integer solution is n1=2

Explanation:

Let's find the answer by using the following equation applied to quadratic polynomials with the form
`an^(2)+bn+c=0`:

`n=\frac{-b\±\sqrt{b^(2)-4ac}}{2a}`

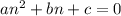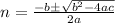
For our case
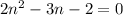`2n^(2)-3n-2=0`, a=2, b=-3, and c=-2, so:

`n=\frac{-(-3)\±\sqrt{(-3)^(2)-(4*2*(-2))}}{2*2}`

`n=(3\±√(9+16))/(4)`

`n=(3\±5)/(4)`

`n1=(3+5)/(4)=2`

`n2=(3-5)/(4)=-0.5`

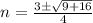
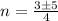
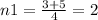
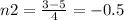
In conclusion, although there are 2 roots (n1, n2), only one of them is an integer, which is n1=2.