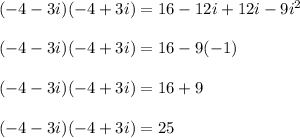Question

What is the product of the complex number z1 and it’s conjugate? PLEASE HELP GRAPH in picture

Answer 1

`(-4-3i) (- 4 + 3i) = 25`

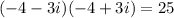
Explanation:

Notice in the graph that z1 has a real component of -4 and an imaginary component of -3.

Then we know that:

`z_1 = -4-3i`

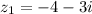
By definition for an imaginary number of the form
`a-bi` its conjugate will always be the number
`a + bi`

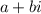
So the conjugate of
`z_1` is:

`-4 + 3i`

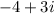
The product of both numbers is:

`(-4-3i) (- 4 + 3i) = 16-12i + 12i-9i ^ 2\\\\(-4-3i) (- 4 + 3i) = 16-9 (-1)\\\\(-4-3i) (- 4 + 3i) = 16 + 9\\\\(-4-3i) (- 4 + 3i) = 25`

Answer 2

The product is 25

Explanation:

we know that

The complex number z1 is equal to

z1=(-4-3i)

we know that

To find the complex conjugate of (-4 - 3i) we change the sign of the imaginary part

so

The conjugate is equal to (-4+3i)

therefore

`(-4-3i)(-4+3i)=16-9(-1)=25`