Question

Convert -sqrt3 - i to polar form. PLEASE HELP. Photo has more information

Answer 1

2cis 7pi/6

Explanation:

Answer 2

-√3 - i ⇒ (2 , 7/6 π)

Explanation:

* Lets explain how to convert a point in Cartesian form to polar form

- Polar coordinates of a point is (r , θ).

- The origin is called the pole, and the x axis is called the polar axis,

because every angle is dependent on it.

- The angle measurement θ can be expressed in radians or degrees.

- To convert from Cartesian Coordinates (x , y) to Polar

Coordinates (r , θ)

1. r = √( x² + y² )

2. θ = tan^-1 (y/x)

* Lets solve the problem

∵ The point in the Cartesian form is z = -√3 - i, where -√3 is the real

part and -i is the imaginary part

∴ The x-coordinate of the point is -√3

∴ The y-coordinate of the point is -1

∵ Both the coordinates are negative

∴ The point lies on the 3rd quadrant

- To convert it to the polar form find r and Ф

∵
`r=\sqrt{x^(2)+y^(2)}`

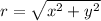
∵ x = -√3 and y = -1

∴
`r=\sqrt{(-√(3)) ^(2)+(-1)^(2)}=√(3+1)=√(4)=2`

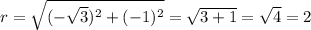
∵ Ф =
`tan^(-1)(y)/(x)`

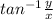
∴ Ф =
`(-1)/(-√(3))=(1)/(√(3))`

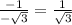
- The acute angle π/6 has tan^-1 (1/√3)

∵ The point is in the third quadrant

∴ Ф = π + π/6 = 7/6 π

- Lets write it in the polar form

∴ -√3 - i ⇒ (2 , 7/6 π)