Answer:
-√3 - i ⇒ (2 , 7/6 π)
Explanation:
* Lets explain how to convert a point in Cartesian form to polar form
- Polar coordinates of a point is (r , θ).
- The origin is called the pole, and the x axis is called the polar axis,
because every angle is dependent on it.
- The angle measurement θ can be expressed in radians or degrees.
- To convert from Cartesian Coordinates (x , y) to Polar
Coordinates (r , θ)
1. r = √( x² + y² )
2. θ = tan^-1 (y/x)
* Lets solve the problem
∵ The point in the Cartesian form is z = -√3 - i, where -√3 is the real
part and -i is the imaginary part
∴ The x-coordinate of the point is -√3
∴ The y-coordinate of the point is -1
∵ Both the coordinates are negative
∴ The point lies on the 3rd quadrant
- To convert it to the polar form find r and Ф
∵
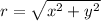
∵ x = -√3 and y = -1
∴

∵ Ф =
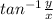
∴ Ф =
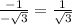
- The acute angle π/6 has tan^-1 (1/√3)
∵ The point is in the third quadrant
∴ Ф = π + π/6 = 7/6 π
- Lets write it in the polar form
∴ -√3 - i ⇒ (2 , 7/6 π)