Answer:
In vertex form it's

In standard form it's
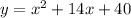
Explanation:
We can use the vertex form to solve for a in

"a" is the number out front that dictates the steepness, or lack thereof, in a parabola. That means that we need h and k (which we have in the vertex) and we need x and y (which we have in the form of one of the zeros). Filling in using a vertex of (-7, -9) and a coordinate point (-7, 0):
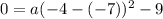 simplifies a bit to
simplifies a bit to
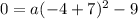 simplifies a bit more to
simplifies a bit more to
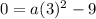 and
and
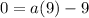 so
so
 ,
,
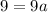 and finally,
and finally,
a = 1
Phew! So there is the a value. Now we can simply fill in the formula completely, using the vertex as our guide:

In standard ofrm that is
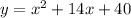
We can check ourselves for accuracy by factoring that standard polynomial using whatever method of factoring you like for quadratics and get that the roots are in fact x = -10, -4
The only reason we needed the zeros is to use one of them as the x and y to solve for a.