Question

Find a polynomial f(x) of degree 4 that has the following zeros.

0, -4, (multiplicity ), 2
Leave your answer in factored form.

Answer 1

`f(x)=(x-2)(x)(x+4)^2`

Explanation:

Since there is a multiplicity at x=-4, that would meant that that part of the factor would have to have an even degree. This means that it would have to be 2.

This would give you
`f(x)=(x-2)(x)(x+4)^2`

Answer 2

`f (x) = x (x + 4)^2(x-2)`

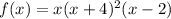
Explanation:

The zeros of the polynomial are all the values of x for which the function
`f (x) = 0`

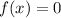
In this case we know that the zeros are:

`x = -4,\ x+4 =0`

`x = -4,\ x+4 =0`

`x = 0`

`x = 2`,
`x - 2 = 0`

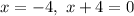
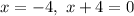
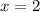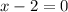
Now we can write the polynomial as a product of its factors

`f (x) = x (x + 4)(x+4) (x-2)`

`f (x) = x (x + 4)^2(x-2)`

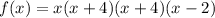
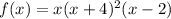
Note that the polynomial is of degree 4 because the greatest exponent of the variable x that results from multiplying the factors of f(x) is 4