Answer:
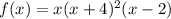
Explanation:
The zeros of the polynomial are all the values of x for which the function
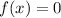
In this case we know that the zeros are:
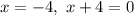
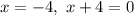
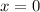
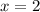 ,
,
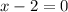
Now we can write the polynomial as a product of its factors
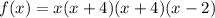
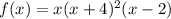
Note that the polynomial is of degree 4 because the greatest exponent of the variable x that results from multiplying the factors of f(x) is 4