Hello!
The answer is:
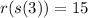
Why?
To solve the problem, first, we need to compose the functions, and then evaluate the obtained function. Composing function means evaluating a function into another function.
We have that:
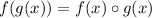
From the statement we know the functions:
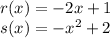
We need to evaluate the function "s" into the function "r", so:
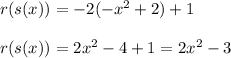
Now, evaluating the function, we have:
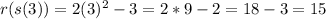
Have a nice day!