Question

PLEASE HELP I ONLY NEED THIS ONE TO FINISH THE SECTION

The functions r and s are defined as follows.

r(x) = -2x + 1

s(x) = -x^2 + 2

Find the value of .

r(s(3))

Answer 1

Hello!

The answer is:

`r(s(3))=15`

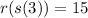
Why?

To solve the problem, first, we need to compose the functions, and then evaluate the obtained function. Composing function means evaluating a function into another function.

We have that:

`f(g(x))=f(x)\circ g(x)`

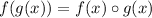
From the statement we know the functions:

`r(x)=-2x+1\\s(x)=-x^(2)+2`

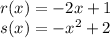
We need to evaluate the function "s" into the function "r", so:

`r(s(x))=-2(-x^2+2)+1\\\\r(s(x))=2x^(2)-4+1=2x^(2)-3`

Now, evaluating the function, we have:

`r(s(3))=2(3)^(2)-3=2*9-2=18-3=15`

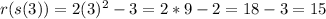
Have a nice day!

Answer 2

The value of r(s(3)) = -21

Explanation:

It is given that,

r(x) = -2x + 1

s(x) = -x^2 + 2

To find the value of r(s(3))

s(x) = -x^2 + 2

s(3) = (-3)^2 + 2 [Substitute 3 instead of x]

= 9 + 2

= 11

Therefore s(3) = 11

r(x) = -2x + 1

r(s(3)) = r(11) [Substitute 11 instead of x]

= -2(11) + 1

= -22 + 1

= -21

Therefore the value of r(s(3)) = -21